
Using the volume of a rectangular prism formula, Solved Example of Volume of a Rectangular PrismĮxample 1: Given the base length of a rectangular prism is 10 cm, the base width is 5 cm, and the height is 15 cm. Some examples of rectangular prisms around us are: There are numerous applications of rectangular prisms. Applications of Rectangular Prism in Real-Life Step 3: Now multiply the base area and the height of the rectangular prism to get the volume. The height of the prism is perpendicular to the base of the prism. Step 2: Next, we will identify the height of the prism. Step 1: Identify the base of the rectangular prism and find its area using the formula. The following steps help estimate the volume of the rectangular prism. To calculate the volume of the rectangular prism, we must first ensure that all the prism dimensions are of the same units.
VOLUME OF A PRISM RECTANGULAR HOW TO
How to Find The Volume of a Rectangular Prism? When we multiply this area by the height of the prism, we get the volume of the rectangular prism. The base of a rectangular prism is a rectangle. The volume of rectangular prism = base area × height of the prism
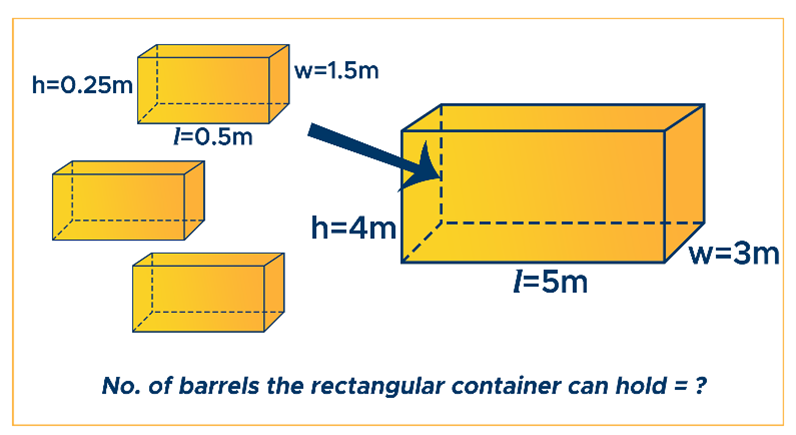
“b” is the base length of the rectangular prism.“l” is the base width of the rectangular prism.Therefore, the unit for the volume of a rectangular prism is cm 3, m 3, and so on. We can obtain the volume of the rectangular prism by multiplying its length, breadth, and height just as we do for a cuboid. The volume of a rectangular prism is defined as the total space occupied by the rectangular prism. What is the Volume of a Rectangular prism? An oblique rectangular prism has parallelograms as its lateral faces.A right rectangular prism has rectangular lateral faces.The pairs of opposite faces of a rectangular prism are identical or congruent.The top and base of the rectangular prism are rectangular.Like a cuboid, it has three dimensions- the base width, the height, and the length.A rectangular prism has a total of 6 faces, 12 sides, and eight vertices.It has two pairs of congruent and parallel bases.A rectangular prism has a rectangular cross-section.The properties of a rectangular prism are as follows: However, we can use the same formula to calculate the volume of the rectangular prism, irrespective of the type of prism. In this case, the height of the rectangular prism is perpendicular drawn from the vertex of one base to the other base of the rectangular prism. On the contrary, in an oblique, rectangular prism, the prism’s bases are not perpendicular to the other faces. It is called a “right rectangular” prism because it has right angles between the base and sides. The base and top of the rectangular right prism are of the same shape and size. It has a polygon as its base while the vertical sides are perpendicular to the base. This prism is in the shape of a geometric solid. There are two main types of rectangular prisms – right rectangular prisms and oblique prisms.Ī right rectangular prism has bases perpendicular to the other faces. Some common names of rectangular prisms are rectangular hexahedron, rectangular parallelepiped, and right rectangular prism. It has six faces, 12 sides, and eight vertices.


This polyhedron has two pairs of congruent and parallel bases. All the faces of the prism are rectangles.
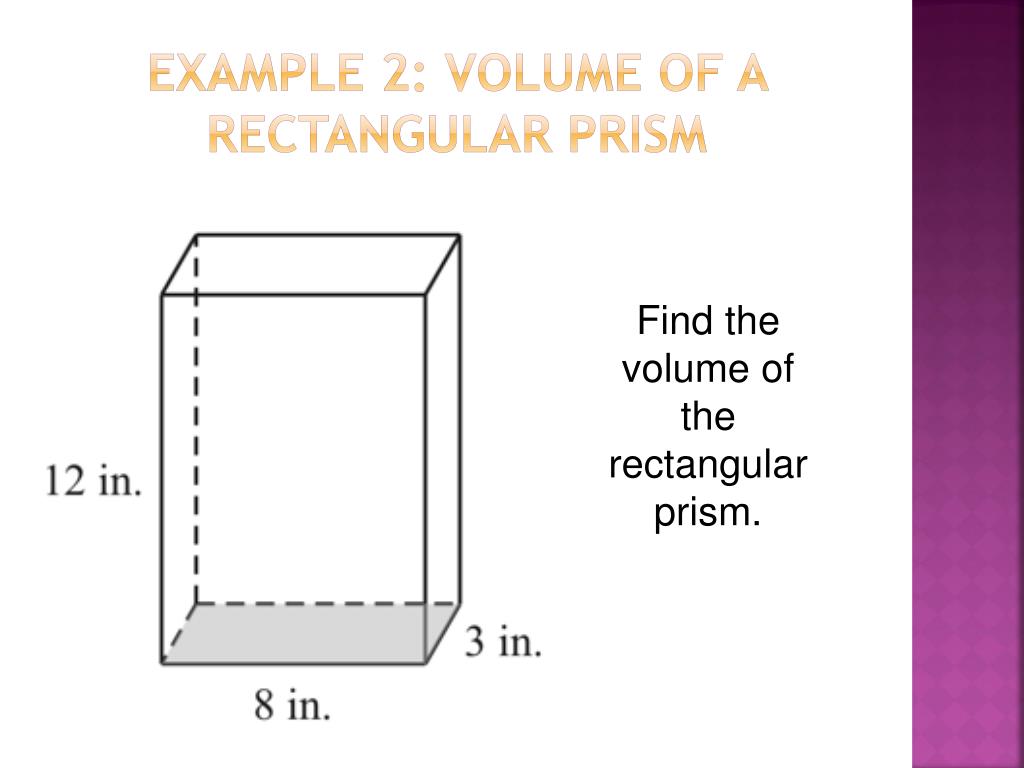
So, if an object has a volume of 1800 cubic units, it means that it is made up of 1800 unit cubes. Volume is the total amount of 3-D space an object occupies.


 0 kommentar(er)
0 kommentar(er)
